CS70-Discrete Math and Probability[2025_Summer-UC Berkley]
课程网页:CS 70 Summer 2025
此课程网页没有存档的说法,如果2025Summer结束,可能会刷新至2025Autumn,因此需要在暑假加紧学习!
课程Calendar
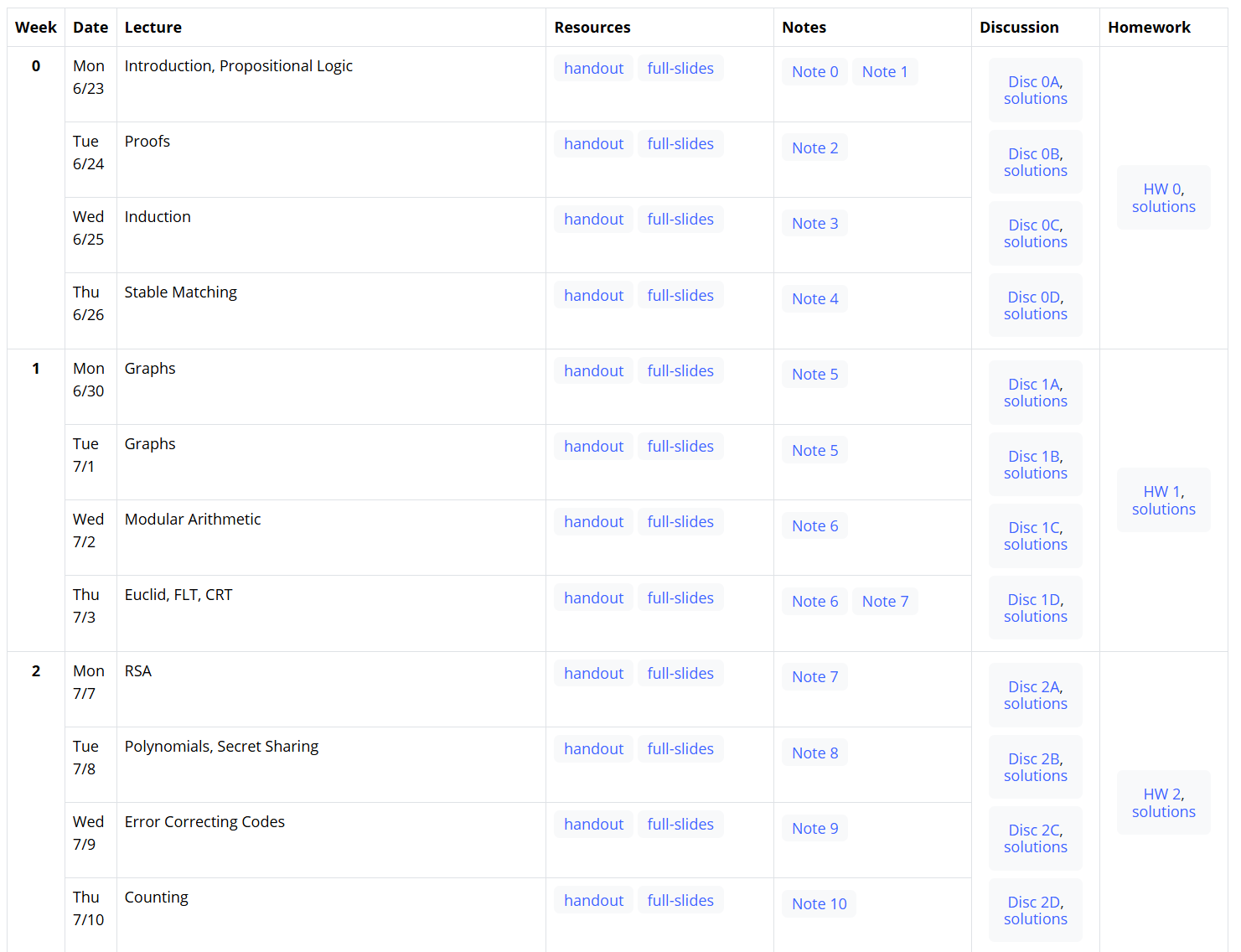
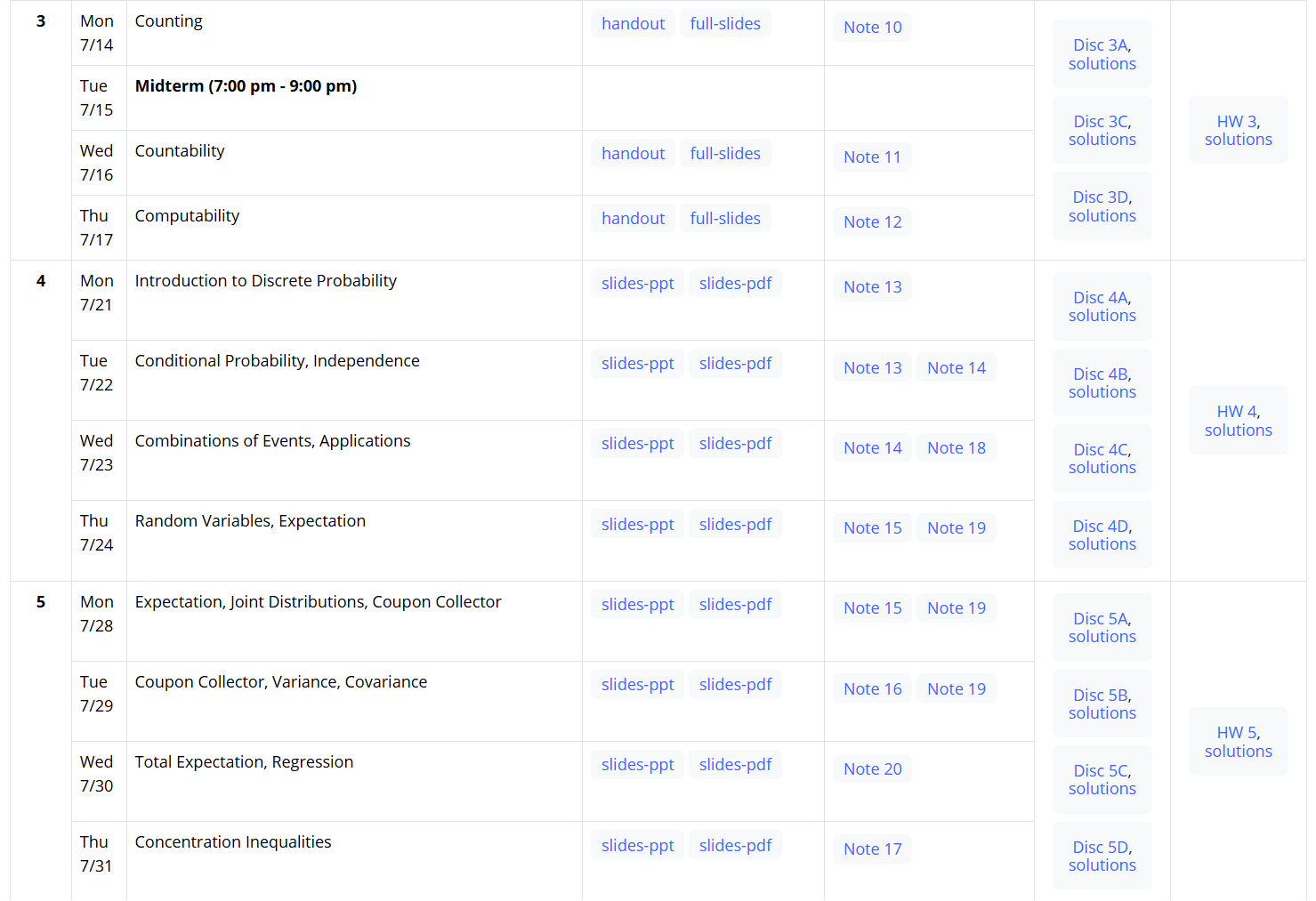
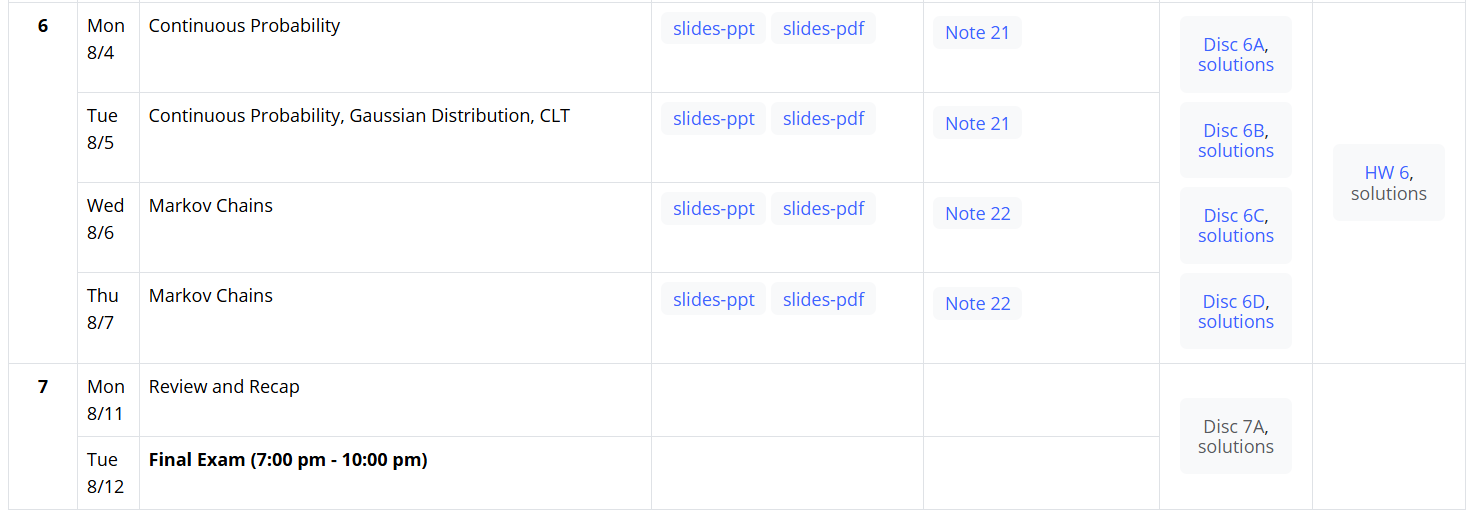
Week 0
Propositional Logic
-
$p \land q$: logical AND
$p \lor q$: logical OR
$\Longrightarrow$: implies
-
When some () embrace definations and list one by one, the last one is conclusion and above are assumptions.
eg. \((\forall x\in\mathbb{Z})\ (\ (((x\in\mathbb{N})\vee(x<0))\wedge\neg((x\in\mathbb{N})\wedge(x<0)))\ .\)
\[(\forall x\in\mathbb{N})\ ((6\mid x)\implies((2\mid x)\vee(3\mid x))).\]eg. $\forall x \exists y P(x,y) \Longrightarrow \exists y \forall x P(x,y) ~~ (\times)$
$ \exists y \forall x P(x,y) \Longrightarrow \forall x \exists y P(x,y) ~~ (√)$
-
Truth table
eg. $(p\lor q)\land r \equiv (p\land r) \lor (q \land r) ~~ (√)$
Stable matching
首先明确几个定义:
-
matching: Disjoint set of $(c_i, j_i)$ pairs that are matched together.
-
Rogue couple: a pair$ (c, j)$ not in the matching that prefers each other over their current matchings
$(c,j’)$and $(c’,j)$.
翻译一下就是,不存在一个rogue pair $(c,j’)$,其中这两个元素各自的真实配对是$(c,j),(c’j’)$. 虽然这两个没有组成一个真实存在的对,但对$c$而言$j’>j$,对$j’$而言$c>c’$.
-
Stable Matching: A matching without rogue couple.
Propose and reject algorithm process: (有的地方称为”Gale-Shapley Algorithm”)
-
Each job proposes to its favorite candidate that hasn’t rejected it; (让job选择未拒绝的优先级最高的candidate)
-
Each candidate rejects all but their favorite job (which they “put on a string”); (candidate接受优先级最高的job,拒绝剩下的)
-
Each rejected job crosses out rejecting candidate from its list; (job把拒掉它的candidate“拉黑”,此后不再分配给他们)
-
Stop when all candidates have a job on a string. (继续操作,直至进程终止,每个人都分到一个job)
下面对这个算法进行分析并给出一些相关结论/定理:
-
A. Termination
一定会终止,并且会在$n^2$步之内终止,理由:每次分配完只有两种情况,a.1人1份job(刚好终止);b.有人没拿到job,相应地,有人拿到了>1份job.
这样终止前,每轮至少消除掉1个job被candidate拒绝的对应关系,而这样的拒绝关系为$n^2$种,于是最后严格$\leq n^2$步.
但我有一个疑惑,为什么不是$n^2-n$步之内?问了AI并没有得到理想的回答,暂且放在这里.
-
B. Improvement Lemma
对每一个candidate而言,收到的job都会随时间推移而逐渐单调变好(注意不是严格单调).归纳法+分配的底层逻辑可证.
-
C.Stability
这是stable的,可以考虑反证法.
我们假设存在一次情况出现了$(c,j)(c’,j’)$,其中对$j$而言$c’>c$,那么实际上$j$应该先于$j’$被分配给$c’$,并且由Improvement Lemma,不会有$c’-j’$且$j$出局的状态,矛盾,所以stable.
-
D.How do jobs and candidates fare?
首先定义x-optimal和x-pessimal,其中$x$指的是job或者candidate中的元素之一:
如果在所有可能的stable matching中,与$x$配对的partner是最优解,则称为x-optimal;
反之最劣解称为x-pessimal.
推广一下就得到了job-optimal, job-pessimal, candidate-optimal, candidate-pessimal,如:
A matching is job optimal if it is x-optimal for all jobs x.
-
E.Job-Optimal of P-R algorithm.
Propose and Reject produces a job-optimal pairing. 也就是我们上面使用的算法是job-optimal,如果想要变成candidate-optimal,只需要把对象换一下就行了.
证明如下:

-
F. Well-Ordering Principle (良序定理)
这个定理的意思是,如果走向变坏,那么一定在这之前有坏事发生
Let t be the first time a job-optimal candidate rejects an offer
…
Before time t, j ∗ hasn’t rejected its optimal match
-
G. one-set instance is not stable and two-set is stable.
这里区分了两种不同的匹配问题,并说明了稳定匹配在这两种情况下的可行性:
Two-set instance(两集合实例):是指两个不同集合之间的匹配,比如:
- 工作 ↔ 候选人
- 医院 ↔ 住院医师
为什么总是存在稳定匹配?
- Gale-Shapley算法保证能找到稳定匹配,且有上文中A. C.定理的保证;
- 这是因为两个不同集合的偏好可以通过propose-reject过程达到平衡
One-set instance(单集合实例)是指同一集合内部的匹配,最典型的例子是:
- Stable Roommates Problem(稳定室友问题)
- 一群人需要两两配对做室友
- 每个人对其他所有人都有偏好排序
为什么可能不存在稳定匹配?举一个4人的例子:
A偏好: B > C > D B偏好: C > A > D C偏好: A > B > D D偏好: A > B > C在这种情况下:
- A最想和B配对,但B更想和C配对
- B想和C配对,但C更想和A配对
- C想和A配对,但A更想和B配对
- 形成了一个”循环偏好”,导致无解
无论怎么分配,总会存在两个人相互偏好对方胜过当前室友,形成rogue pair.
-
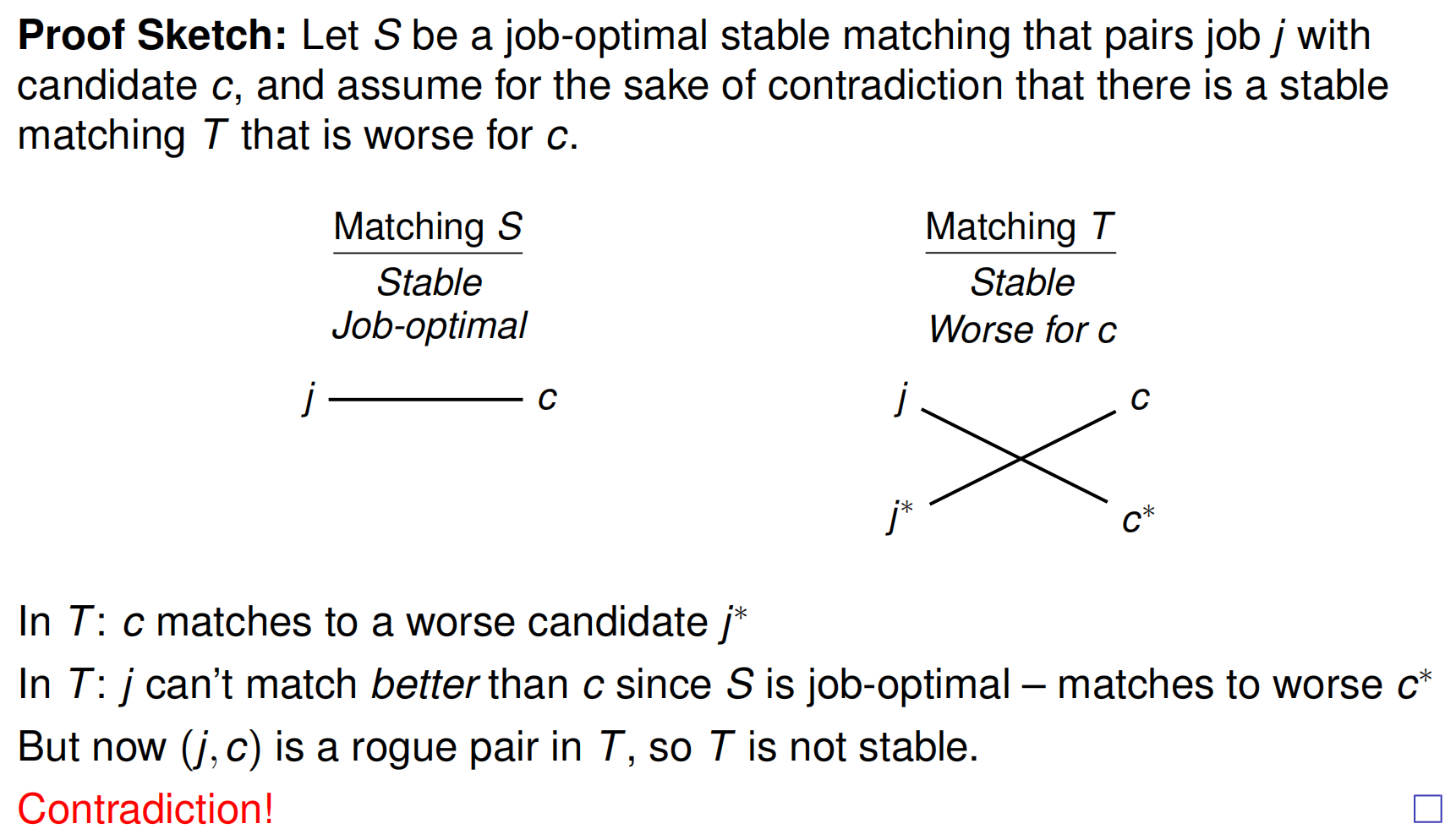
H. Job-Optimal and Candidate-Pessimal
这个定理内容是:If a stable matching is job-optimal, then it is candidate-pessimal.
证明:这里一般用的是反证法